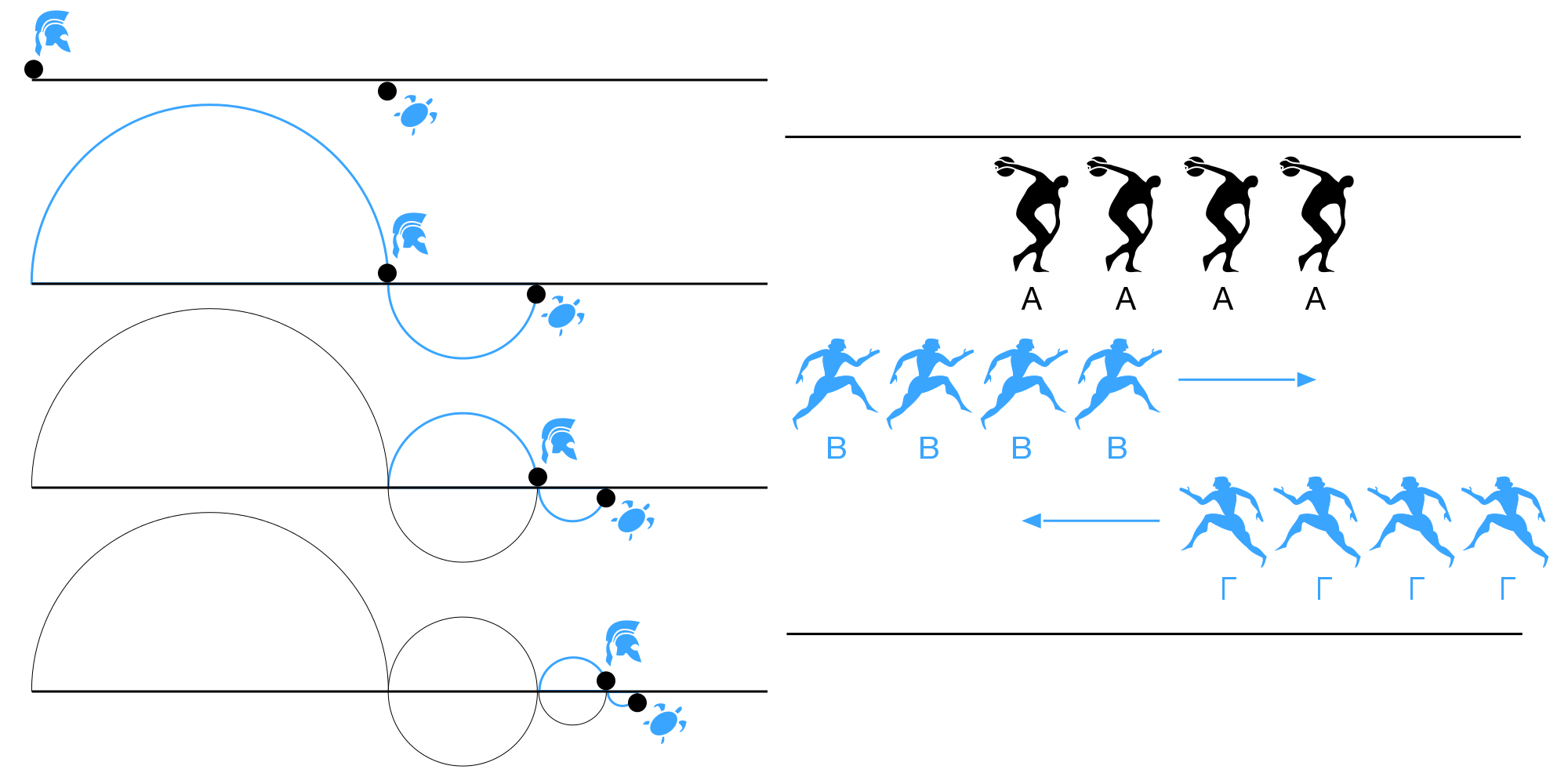
Note: tous les schémas des paradoxes de Zénon proposés plus bas sont librement réutilisables selon les termes de la licence CC-BY avec un lien vers ce billet.
À l’heure des premières hypothèses atomiques, les penseurs sont confrontés à un renouveau de la question de la continuité de la matière, problème aussi vieux que la philosophie. En effet, les avancées scientifiques, quel que soit le domaine d’étude, posent toutes ce problème en cette fin de XIXe siècle. La physique s’interroge sur la constitution de la matière, remettant en cause l’existence d’une particule atomique première, la biologie porte son questionnement sur la continuité ou la discontinuité de l’évolution, enfin, les mathématiques, confrontées aux théories cantoriennes sur les ensembles voit ses chercheurs se diviser entre tenants du finitisme ou de son contraire. Ces hypothèses ne sont toutefois qu’une étape dans un long débat qui a agité la philosophie depuis l’Antiquité jusqu’à la Modernité à laquelle appartient Bergson. Ce dernier va dégager la question inhérente à ces domaines mathématiques, biologiques et physiques pour en extraire le problème fondamental et l’appréhender directement.
Au XIXe siècle, le problème avait déjà été étudié par des philosophes, en particulier Lachelier, Spencer et Cournot. Ces trois penseurs semblent avoir retenu l’attention de Bergson qui s’est inspiré de leurs démarches. Il l’avoue lui-même à Jean de La Harpe : Un jour, j’ai découvert Le fondement de l’induction de Lachelier, aujourd’hui très oublié : un livre magnifique ! (…) Je dois énormément à la dialectique de Lachelier. Ensuite, j’ai découvert l’Essai de Cournot que j’ai lu et relu avec prédilection (…). De Cournot j’ai passé à Spencer, dont j’ai été un admirateur convaincu1. Bien que ne partageant pas les mêmes conclusions, ces trois auteurs ont la particularité de mettre le problème de la continuité de l’expérience au centre de leurs investigations philosophiques. Cette question avait déjà été posée quelque vingt-cinq siècles auparavant par Zénon l’Eléate (début du Ve siècle av. J.-C.), disciple de Parménide, elle va être reprise par Bergson à la fin du dix-neuvième siècle.
Dans ce billet, nous aborderons les paradoxes de Zénon et leurs conséquences pour le débat du continu puis nous étudierons la réponse de Bergson face à ces arguments.
Le problème du continu tel qu’il est posé par Zénon
Zénon d’Elée (Wikimedia Commons, Jeremy Weate)
La connaissance que nous avons de la philosophie de Zénon est fragmentaire. Le témoignage le plus fiable sur la vie et l’œuvre du présocratique reste très vague quant à l’œuvre du philosophe. Dans ce passage du Parménide, Platon nous dit que Socrate alla écouter Parménide et Zénon dans l’espoir d’entendre la lecture du traité de Zénon : car c’était la première fois que Parménide et Zénon apportaient l’œuvre à Athènes2. La suite du texte et une question du jeune Socrate nous laisse penser que le « traité » dont il est question a pour thèse l’affirmation de l’unicité des choses. Cette pensée toute parménidienne va beaucoup influencer Zénon, on verra son implication dans les paradoxes.
D’après Aristote, seul philosophe antique à être revenu sur les positions de Zénon, les arguments cinématiques du présocratique sont au nombre de quatre3. Certaines sources font état de quarante arguments tendant à établir l’unicité de l’Être plus cinq arguments tendant à son immobilité, mais l’absence de fragments les concernant ne nous permet pas de juger de l’authenticité de cette affirmation. Il se peut que les quatre arguments présentés par Aristote aient été sélectionnés par l’auteur parce que formant un tout et étant représentatifs de l’idée qu’il se faisait de la pensée de Zénon.
Paradoxe 1 : le stade (ou la dichotomie)
Cet exposé de l’énigme est particulièrement bref, on peut toutefois constater le raisonnement logique suivant :
- (1) Le coureur doit passer par une pluralité infinie de points alignés selon la suite mathématique 1/2, 1/4, 1/8, 1/16, …
- (2) Il est impossible pour un mobile quelconque de toucher cette pluralité infinie de points en un temps fini.
- (1 et 2) Donc, le coureur n’atteindra jamais son but.
Pour Aristote, la solution à ce problème réside dans les prémisses (2). Pour lui, un temps défini est parfaitement divisible, de la même manière que l’espace a été ici divisé. Un temps divisible à l’infini est donc suffisant pour le coureur pour toucher l’infinité de points qui le séparent de l’arrivée. Aristote ne croit du reste pas en la possibilité de l’existence de cette infinité de points « en acte », l’existence de ces points ne serait que potentielle. La question de l’impossibilité de l’existence d’une division infinie est donc ici posée par Aristote, elle va alimenter le débat sans fin de la philosophie à tel point qu’il est difficile de dire de cette impossibilité si elle est logique ou tout simplement physique.
Paradoxe 2 : l’Achille
La structure de l’argument est donc la suivante :
- (1) Achille et la tortue font tous deux des courses simultanées, ainsi, leur nième course commence et finit en même temps.
- (2) Puisque Achille suit la tortue avec un temps de retard, la nième course de la tortue aura la même longueur que la (n+1)ième d’Achille.
- (3) On considère qu’Achille a rattrapé la tortue si et seulement si une de ses courses le fait aboutir sur un point atteint en même temps par sa rivale.
- (4) Selon (2), la fin de la course verra la tortue gagner avec un intervalle d’avance.
- (5) Donc, selon (3), Achille n’a aucune chance de la rattraper un jour !
Comme pour le coureur du stade, les écarts entre les points à atteindre par Achille se réduisent petit à petit pour atteindre des valeurs infinitésimales. Pour autant que les deux coureurs aient des vitesses constantes (ce qui semble être le cas à la lecture d’Aristote), la séquence décrite est une progression géométrique qui tend vers la valeur zéro. Ainsi, la remarque critique d’Aristote est justifiée, il s’agit bien d’une version plus spectaculaire du paradoxe du stade. En effet, L’Achille pose la même question de divisibilité infinie de l’espace, en y rajoutant la question de la divisibilité du temps qui s’y voit corrélée.
Paradoxe 3 : la flèche
On peut en tirer l’argumentation logique suivante :
- (1) Une chose est considérée comme étant en repos lorsqu’elle occupe un espace qui est de sa taille.
- (2) En tout moment, la chose mouvante est dans l’instant
- (3) Quand une chose est dans l’instant, elle occupe une place qui est de sa taille.
- (4) donc, la flèche est immobile dans son déplacement !
Ici, Zénon ne traite plus de la divisibilité à l’infini du temps ou de l’espace (il part du reste du principe qu’ils ne sont pas infiniment divisibles) mais pose la question de la succession des instants. Quel est donc le lien entre tous ces petits « maintenants » ? Pour Zénon, il est évident qu’il s’agit de montrer que ce qui est valable pour une chose à chaque instant d’une durée de temps l’est aussi à travers toute cette durée (ici, il importe peu de savoir si ces moments sont formés d’instants indivisibles ou pas). Dans ce paradoxe, Zénon met en évidence la valeur du présent, sous la forme d’une ligne de séparation claire entre passé et futur. En effet, si l’espace est indivisible et le temps aussi, on ne peut pas dire se trouver dans un lieu puis dans un autre puisque ces deux lieux sont inséparables.
Paradoxe 4 : les rangées en mouvement
Ce quatrième paradoxe, plus compliqué que les précédents, fait l’objet d’une longue description de la part d’Aristote que nous ne reproduirons pas ici mais à laquelle nous renvoyons7. Ce texte d’Aristote décrit la course de deux rangées de coureurs dans un stade qui se croisent. Il a été l’objet d’un commentaire de Simplicius qui nous livre le diagramme ci-contre8.
Nous sommes en présence d’une situation que notre esprit a de la peine à comprendre instantanément. En effet, comment se fait-il que certaines distances semblent être parcourues deux fois plus rapidement que d’autres alors que les vitesses des mobiles sont supposées constantes ? En effet, le premier B (rangée en mouvement vers E) ne met, pour passer devant la moitié de la rangée des A (immobiles) seulement la moitié du temps que le premier Γ (rangée en mouvement vers Δ) pour passer devant les B. Selon ce paradoxe, chaque espace serait égal au double de lui-même et à la moitié de lui-même, ce qui ne fait pas sens.
Le résultat de ces paradoxes mène à l’absurde : si le continu est divisible à l’infini (1 et 2), alors on se trouve face à une impossibilité logique, mais si le continu est composé d’indivisibles, alors le mouvement est contradictoire car chaque partie de la continuité devrait valoir toutes les autres parties !
De manière générale, on peut constater que Zénon soumet toujours l’unicité de l’être au raisonnement mathématique. Si tout ce qui existe est réellement divisible à l’infini, il ne peut rien subsister d’Un. Aucune chose ne peut donc exister, ni en soi, ni dans les intervalles de la réalité divisée (le monde n’est-il composé que de vide ?). Le disciple de Parménide pose tout de même une question extrêmement pertinente au travers de ses arguments ardus : comment peut-il y avoir de changements réels au sein de l’être ? Le problème est posé, Zénon aura réussi à faire discourir des générations de penseurs après lui.
Le débat autour de la proposition de Zénon et son évolution
Platon (Wikimedia Commons, Marie-Lan Nguyen)
Platon sera le premier à reprendre la discussion lancée par Zénon, parce qu’il y voit la mise en cause du Multiple. En effet, Zénon montre que le franchissement de la multiplicité est impossible et que l’introduction du Multiple dans le cosmos est absurde. Les arguments de Zénon vont donc dans le sens de l’établissement par Platon de l’identité de l’Etre et de l’Un.
Aristote (Wikimedia Commons, Jastrow)
Aristote, lui, mettra plus de temps à prendre une position claire vis-à-vis des thèses de Zénon, à l’image de sa Physique dans laquelle les paradoxes sont cités plusieurs fois avec chaque fois une réfutation différente. Aristote oppose au problème de la pluralité de points des premiers paradoxes l’infinité des instants qu’a à disposition le mobile pour parcourir la distance (l’infini du temps couvre l’infini de l’espace). Ensuite, il se ravise et se demande si ce n’est pas la façon de poser le problème qui brouille les pistes, le Continu est en effet toujours présenté comme réductible à des éléments discontinus.
Après ces premières critiques, Aristote en vient à affirmer que le mouvement est quelque chose de donné et qu’il faut accepter l’Etre sous deux formes : l’Etre en puissance et l’Etre en acte. Ainsi, l’espace et le temps permettent de mesurer le mouvement a posteriori, se contenter de le constater sans prouver son existence ni l’invalider. Thomas d’Aquin, au XIIIe siècle, suit Aristote dans ses conclusions sans s’aventurer plus loin dans le débat. Il considère avant tout les paradoxes de Zénon comme des sophismes brillants.
Descartes (Wikimedia Commons, André Hatala)
Leibniz (Wikimedia Commons)
C’est ensuite au tour de Descartes de reprendre le problème au XVIIe siècle. Bien que conservant l’interprétation cosmologique des arguments, sa démarche est toute différente de celles de ses prédécesseurs : il fait appel aux mathématiques. Posant les premières bases du calcul intégral, il tente d’établir une relation arithmétique entre les éléments discontinus et continus, il cherche à intégrer les premiers dans des formules continues. La mathématisation du problème ne le résout qu’en apparence, fictivement dans des formules, le problème n’est donc pas clos. En 1676, Leibniz introduit en mathématiques un nouvel outil de calcul : le calcul infinitésimal. Cet outil permet, d’après lui, la résolution des apories de Zénon en « intégrant » la somme infinie des points de l’espace et celle, aussi infinie, des mouvements disponibles au mobile. Le problème réside dans le fait que la signification épistémologique d’un tel calcul pose un problème aux penseurs de l’époque. Le débat se recentre donc sur cette question et perd le questionnement présocratique.
Pour sortir du questionnement mathématique, il faudra attendre Renouvier qui, en 1851, contestera enfin l’approche mathématique (en vigueur de Descartes à Stuart Mill). Pour lui, le problème n’est pas une question de formalisme rigoureux mais d’intuition. Le débat reprend alors de l’ampleur et toutes les solutions imaginables sont échafaudées, toutes les mathématiques ont droit à leur remise en cause. On en arrive à la conclusion que le mouvement ne se donne pas à la connaissance humaine. Et c’est ici que Bergson intervient, introduisant dans la discussion un nouveau mode de connaissance que l’intelligence, redonnant de l’air au débat étouffé par trop d’années de stagnation.
Bergson et les arguments de Zénon
Bergson (Wikimedia Commons)
C’est donc dans une direction nouvelle que Bergson va appréhender les paradoxes posés par Zénon. Pour le philosophe, Zénon n’attaque pas la réalité du mouvement, pas plus que celle du continu, mais s’en prend bel et bien à l’intelligence humaine. En effet, c’est du côté de l’intérieur qu’il faut chercher la solution au problème millénaire. Bergson oppose ainsi la vie de la conscience, durée intérieure qualitative à l’idée de l’espace extérieur, entièrement composé de quantités mesurables scientifiquement.
Bergson donne l’image de la mélodie pour expliciter son propos : on peut en effet y trouver deux réalités, la perception de chaque note séparée, spatialisées, comptables, ou le produit d’un acte de l’esprit qui ne donne pas pour produit fini une suite de vibrations distinctes mais au contraire une multiplicité continue, une mélodie ressentie. La durée toute pure est la forme que prend la succession de nos états de conscience quand notre moi se laisse vivre, quand il s’abstient d’établir une séparation entre l’état présent et les états antérieurs9. La succession des notes doit donc être perçue comme une « pénétration mutuelle » d’éléments qui ne s’isolent les uns des autres que quand l’intellect vient les en abstraire. Voir des points juxtaposés, homogénéiser la durée, c’est déjà introduire la notion d’espace dans la mélodie, dans ce qui dure. Comme le bruit régulier du balancier qui invite l’homme au sommeil, ce n’est jamais un coup distinct qui plonge l’individu dans les bras de Morphée mais réellement la continuité du battement. Ainsi, chaque surcroît d’excitation s’organise avec les excitations précédentes10, et c’est cela qui produit un effet.
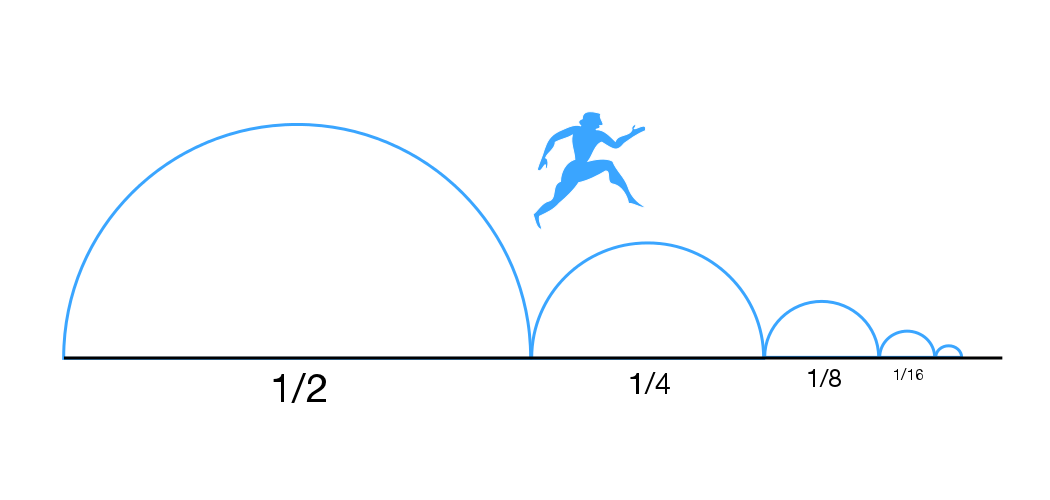Il en va de même pour le mouvement : nous éprouvons premièrement qu’il a lieu dans l’espace, on pense donc immédiatement à la distance parcourue du départ à l’arrivée sous la forme d’une succession de points, de positions distinctes. Ces dernières ne sont en fait que des illusions, elles sont immobilité pure ! La réalité du mouvement, elle, est une synthèse pour ainsi dire qualitative, une organisation graduelle de nos sensations successives les unes avec les autres11. Il en va de même pour l’exemple des coups de cloche12 qui se fondent les uns dans les autres dans la conscience, leur effet total diffère qualitativement de l’effet que nous en aurions s’il nous venait à l’idée de les compter. Nous percevons le mouvement quand nous percevons une force, une sorte de poussée, pas un simple parcours. Bergson donne aussi l’exemple de l’étoile filante dont on voit la traînée encore quelques instants après son passage. Zénon est en fait victime d’une confusion entre la sensation intensive du mouvement et sa représentation extensive dans l’espace. Zénon oublie qu’on peut bien diviser une chose, mais non pas un acte13.
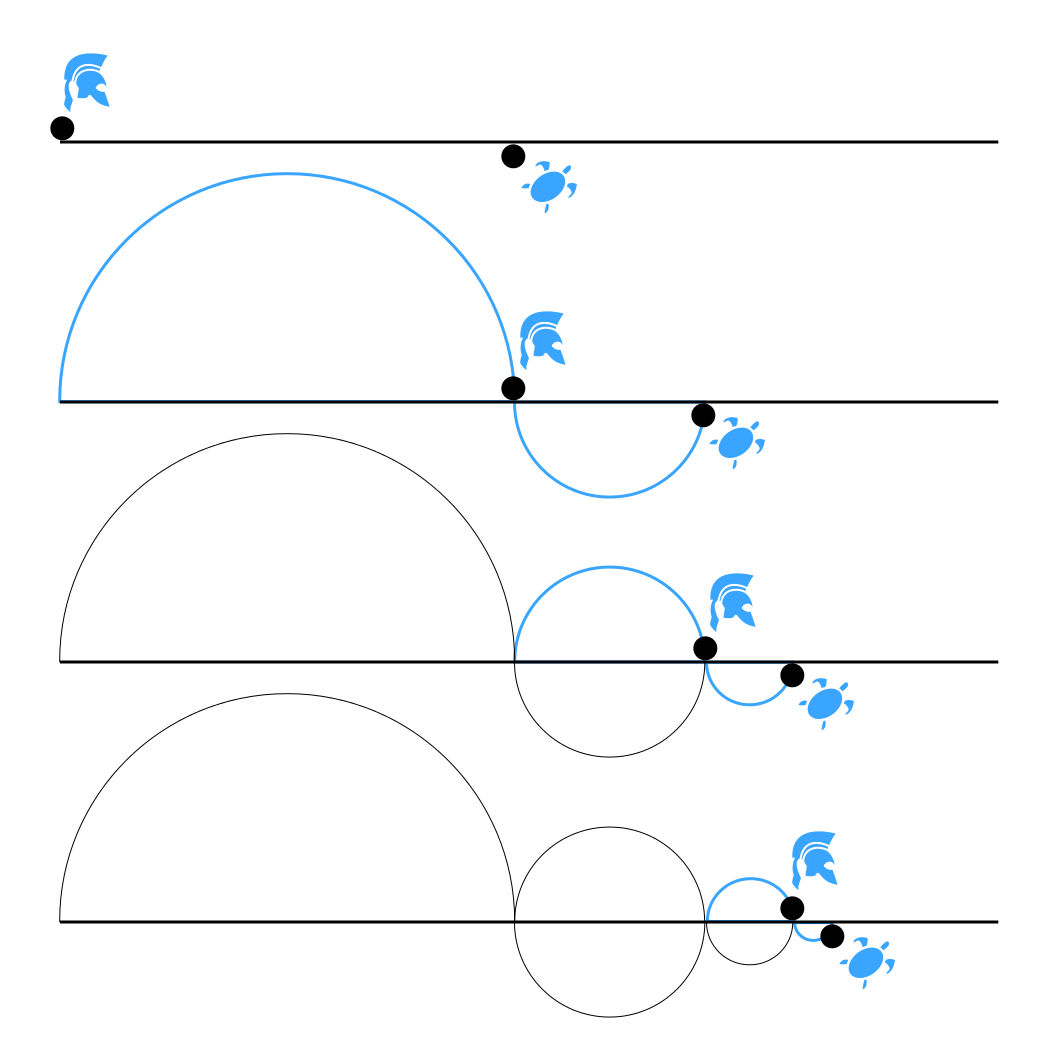Pour en revenir aux exemples concrets des paradoxes éléates, Bergson conçoit parfaitement qu’un intervalle est divisible à l’infini, mais la vérité est que chacun des pas d’Achille est un acte simple, indivisible, et qu’après un nombre donné de ces actes, Achille aura dépassé la tortue. L’illusion des Eléates vient de ce qu’ils identifient cette série d’actes indivisibles et sui generis avec l’espace homogène qui les sous-tend14. Ainsi, justifié par la divisibilité de l’espace homogène, Zénon se permet de reconstituer le mouvement d’Achille avec les pas de la tortue (les actes des deux mobiles se confondent donc dans une même catégorie). Bergson ne juge donc pas utile le recours à des arguments métaphysiques pour démonter la théorie de Zénon (qui visent à montrer la limite de la divisibilité de l’espace), il suffit de voir le mouvement comme étant durée plutôt qu’étendue, qualité et non pas quantité15. Le présocratique commet donc l’erreur de solidifier le mouvement comme acte de l’esprit, comme une ligne qu’il projette hors de l’homme. Mais l’intervalle n’existe que pour nous, à cause de la pénétration mutuelle de nos états de conscience. La saisie de la pensée présuppose une conscience capable de faire s’articuler le passé, le présent et l’avenir de façon solidaire.
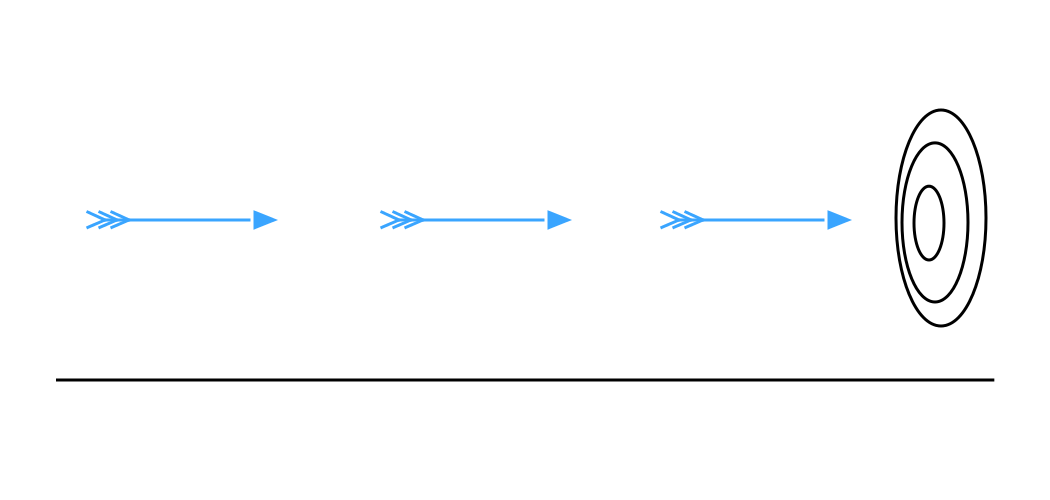Les mathématiques ne sont donc pas propres à appréhender le vrai mouvement puisqu’elles excluent la durée de leur champ de connaissance. Pire, si la mécanique ne retient du temps que la simultanéité, elle ne retient du mouvement lui-même que l’immobilité16! Bergson constate que les formules mathématiques n’expriment que des faits accomplis, expliquent les phénomènes a posteriori. En algèbre, lors du calcul d’un différentielle, c’est toujours à une extrémité de l’intervalle que la mathématique se place17. La division vient toujours après le mouvement.
Bergson fait l’expérience du déplacement de sa main de A en B et fait la constatation suivante : Ma conscience me donne la sensation intérieure d’un fait simple, car en A était le repos, en B est le repos encore, et entre A et B se place un acte indivisible ou tout du moins indivisé, passage du repos au repos, qui est le mouvement même18. C’est la vue qui, ensuite, semble diviser le mouvement. Mais, si elle divise réellement quelque chose, c’est de la ligne supposée parcourue qu’il s’agit, et pas le mouvement en lui-même (en bref, la trace de l’étoile filante et pas son mouvement). Il ne faut donc pas tomber, comme Zénon, dans le piège qui consiste à confondre les données des sens, qui perçoivent le mouvement, avec les artifices de l’esprit qui le recompose19.
Le problème de Zénon est donc mis au jour par Bergson, il ignore que le mouvement est un fait indivisé ou une suite de faits indivisés, tandis que la trajectoire est indéfiniment divisible20.
Bilan : les instantanés ne contredisent pas la continuité
Finalement, on peut observer que Bergson aboutit à la conclusion que le continu et le mouvement existent bel et bien. C’est parce que le Continu ne peut se réduire au Discontinu (c’est-à-dire au ponctuel), que le Mouvement ne peut se réduire au Statique21. Il résume du reste admirablement sa position à propos du Continu dans un de ses ouvrages plus tardif, Durée et simultanéité :
Prédécesseur de Zénon d’Elée, Héraclite d’Ephèse avait, lui aussi, son avis sur la question du continu. Le flux continuel de toute chose souligne la continuité absolue du changement, du mouvement, de la vie :
[hr]
- Déclaration citée dans : MILET, Jean, Bergson et le calcul infinitésimal, Paris, PUF, 1974, page 38 ↩
- PLATON, Parménide, 127a (DK 29 A 11) cité in KIRK, G.S., RAVEN, J.E., SCHOFIELD, M., Les philosophes présocratiques, Fribourg : Editions Universitaires de Fribourg, 1995, p.257 ↩
- Aristote en fait mention et les commente dans le livre VI.9 de la Physique (239b) (DK 29 A 25) ↩
- ARISTOTE, Physique, VI.9 239b9 cité in CAVEING, Maurice, Zénon d’Elée, Prolégomènes aux doctrines du continu, Paris : Vrin, 1982, p.66 ↩
- ARISTOTE, Physique, 239b14 in CAVEING, op. cit. p.79 ↩
- ARISTOTE, Physique, 239b30 in KIRK et alii, op. cit p. 293. ↩
- ARISTOTE, Physique VI.9 239b33 (DK 29 A 28) Texte en ligne ici ↩
- SIMPLICIUS, Physique 1016,14 in KIRK et alii, op cit p. 296 Le diagramme est une figure vraisemblablement empruntée à Alexandre. ↩
- BERGSON, Henri, Essai sur les données immédiates de la conscience, Paris : PUF, 2005, p.74-75 ↩
- BERGSON, Essai, p. 79 ↩
- BERGSON, Essai, p. 83 ↩
- BERGSON, Essai, p. 95 ↩
- BERGSON, Essai, p. 83 ↩
- BERGSON, Essai, p. 84 ↩
- BERGSON, Essai, p. 85 ↩
- BERGSON, Essai, p. 88 ↩
- BERGSON, Essai, p. 89 ↩
- BERGSON, Henri, Matière et mémoire, Paris : PUF, 2004, p. 209 ↩
- BERGSON, MM, p. 211 ↩
- BERGSON, MM, p. 214 ↩
- MILET, op. cit. p. 58 ↩
- BERGSON, Henri, Durée et simultanéité, Paris : Librairie Félix Alcan, 1929, p. 54 ↩
- HERACLITE, fragment 12(deux premières lignes) cité par Arius Didyme dans Eusèbe et fragment 91 cité par Plutarque. in KIRK et alii, op cit p. 207 ↩
Trackbacks/Pingbacks